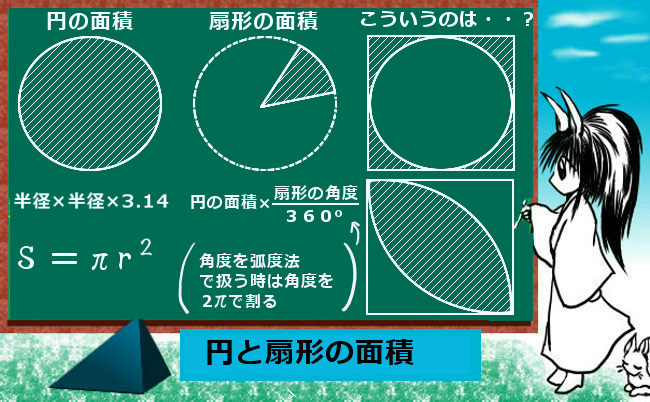
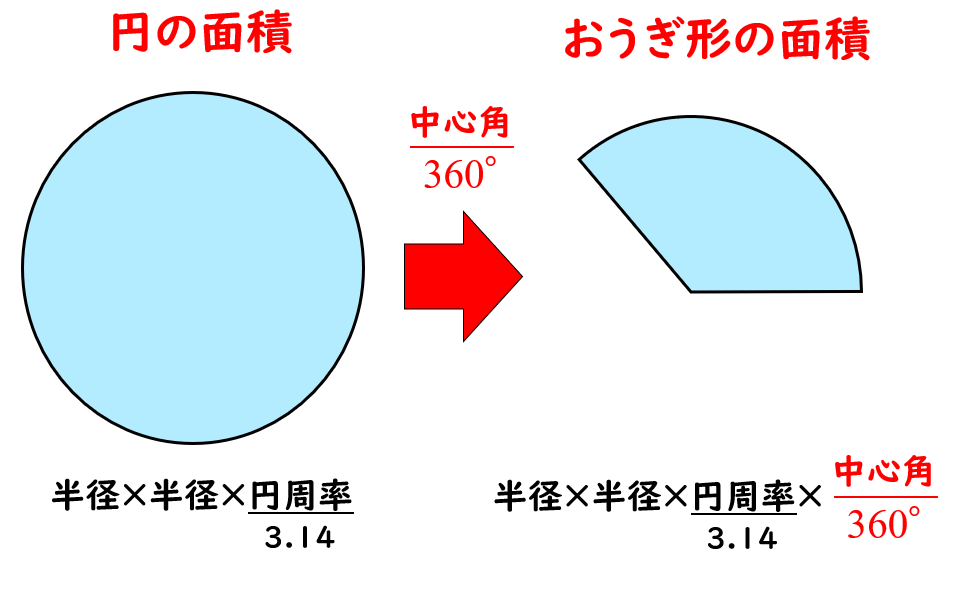
扇形の面積の求め方の公式! 「 おうぎ形の面積の求め方 」はつぎの公式であらわされるんだ。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360 になるんだ。半径が 32(cm)の円の面積を求めてください。ただし円周率を 314とします。 円の面積を求める公式は 円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率 なので、円の面積を \(S\) とすると \円の面積と周の長さの公式 これは覚えておくしかありません。 中学生には導くことができないのです。 ただ、これは小学校の時の算数で、 円周の長さは、『直径×\(\,314\,\)』 円の面積は、『半
小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ
おうぎ 円 の 面積 公式
おうぎ 円 の 面積 公式-公式の2行目に書いた通り、扇形の面積は、半径 r と弧の長さ l が分かっている場合、次の式で簡単に求められてしまいます。 S = 1 2lr S = 1 2 l r 半径と中心角から面積を求める式から、上の式を導円・おうぎ形の公式をまとめて問題解説! 応用影の部分の面積、周の長さの求め方! おうぎ形の中心角を求める3つのパターン! おうぎ形の周りの長さを求める方法とは? ←今回の記事 おうぎ




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ
V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 扇形とは? 面積・弧の長さ・中心角・半径の公式と求め方 この記事では、「扇形(おうぎ形)」についてできるだけわかりやすく解説していきます。 扇形の面積や弧の長さの公式(度円の面積を求める公式に代入して、計算すればいいだけですね。 求める面積 S は S = πr2 = π× 32 = 9π S = π r 2 = π × 3 2 = 9 π 中学生以上なら円周率を文字 π で表してよいですが、小学生の場合は
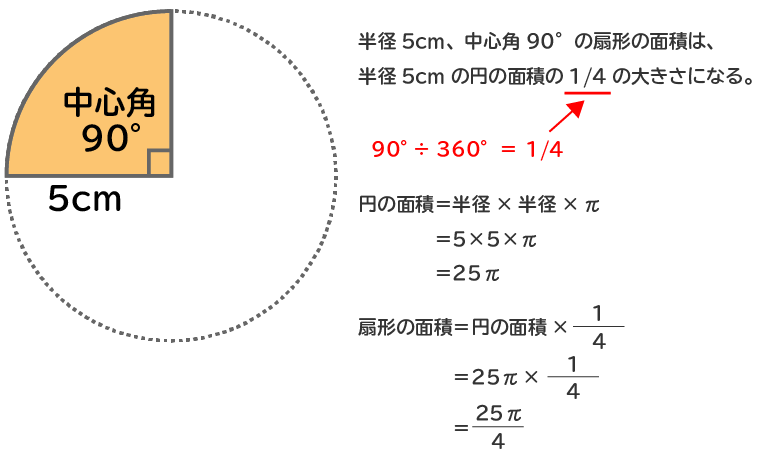
中学1年数学 円とおうぎ形の計算 円の周の長さと面積・・・半径γの円の周の長さをℓ、面積をSとすると、 ℓ=2πγ S=πγ² この赤いおうぎ形は大きな円の4分の1になっています。 円の半径は正方形の一辺と同じなので1cmです。 従ってこのおうぎ形の面積は1×1×314÷4=0785ですね。 そこからこの青い三 扇形の面積を求める公式を導出する 円錐の側面積 = LRπ で求めることができることがわかりましたが、この式を変形してみます。 式を変形 小文字になってしまっていますが気にし
まずは、円の面積と円周の求め方をおさらいしましょう。 円の面積 半径 $×$ 半径 $×$ 円周率($314$) ですが、中学では、半径 $=$ $r$ , 円周率 $=$ $π$ として、次のように表します。扇形面積=円の面積×( 扇の内角/360°) 三角形の面積=( 半径 2 ×sin扇の内角 )/2 ・・・二辺夾角法 扇の面積-三角形の面積=円弧の面積 WingneoのIAの計算方法 円弧の始点・終点2点の座標 扇形の面積を求めるときには次の公式を使います。 扇形の面積 =半径×半径×円周率× ※扇形の面積は、円の面積に をかけることで求めることが出来ます。 ※円周率は、小学校ではふ




扇 おうぎ 形の面積を求める公式と弧の長さの求め方




美和柄素材 扇散らし おうぎちらし Japanese Mon Iuen
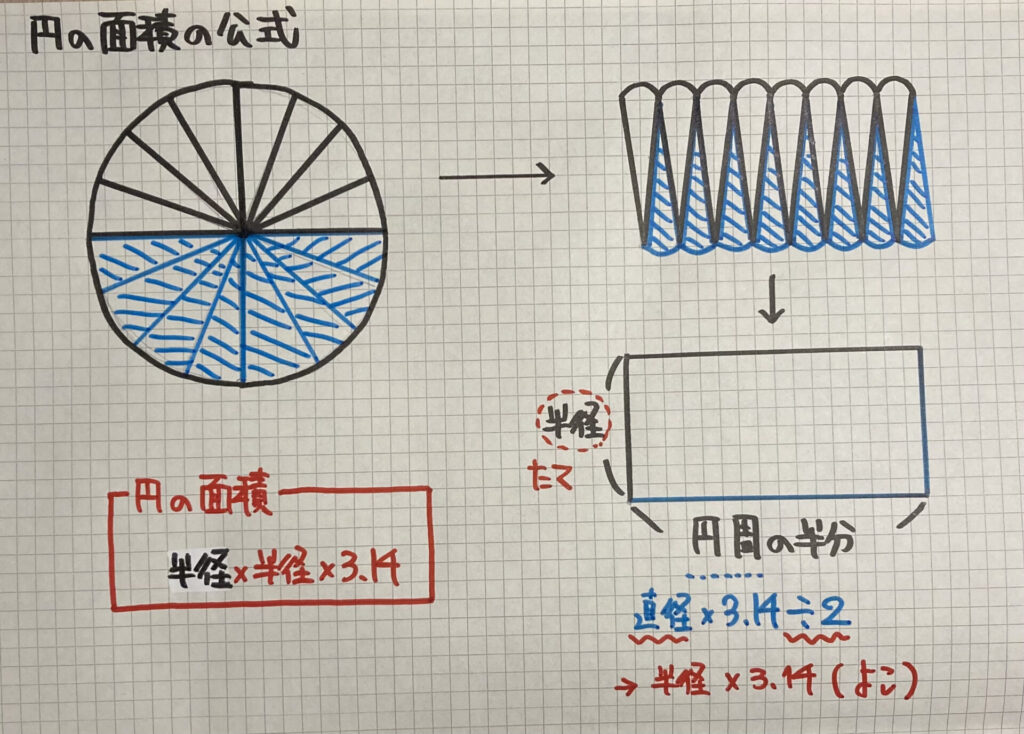
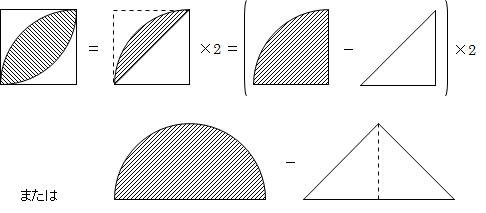
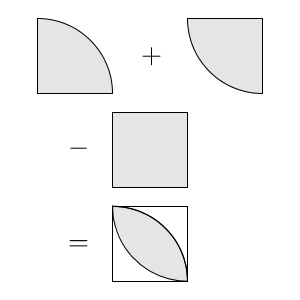
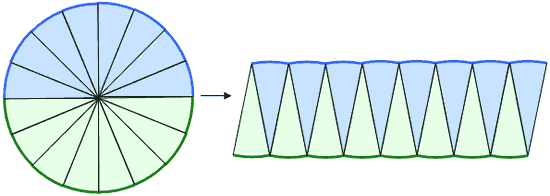
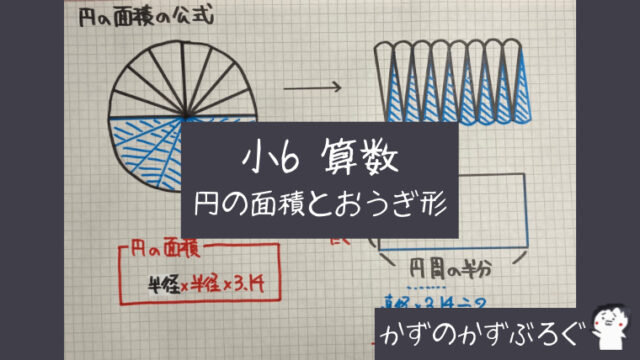
学習のポイント 正方形とおうぎ形を合わせた形の面積を素早く求められるようにしましょう。 *色のついた部分の面積を求めます。 4分の1のおうぎ形2つから正方形をひく、4分の1のおうぎ形は円の一部であり、以下の公式も「円の一部」という意味の式になっています。 \(弧の長さ=円周×\) \(\frac{中心角}{360}\) \(おうぎ形の面積=円の面積×\) \(\frac{中心角}{360}\) おうぎ形の こちらで確認してくださいね 小6算数「円の面積とおうぎ形」の問題 どこよりも簡単な解き方・求め方 「円」を等分(同じ大きさに分ける)して細かく細かくしていって並べか



基本 おうぎ形などの面積 なかけんの数学ノート



小5の学習ポイント2 円とおうぎ形 前田昌宏の中学受験が楽しくなる算数塾
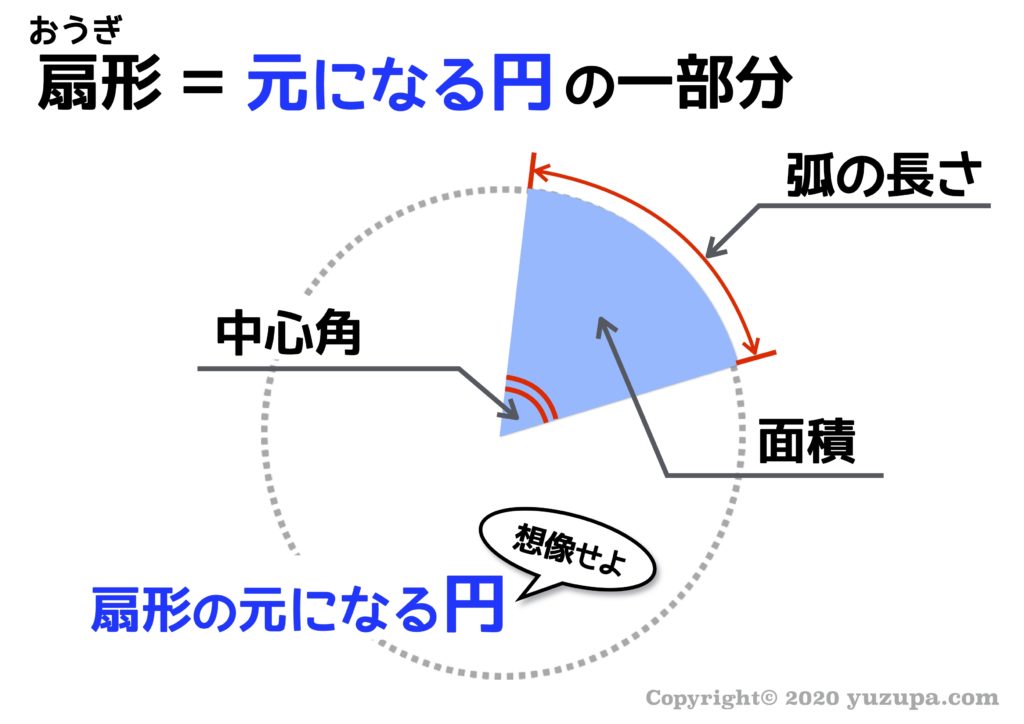
円の面積のまとめ ・円の面積=半径×半径×314 ・おうぎ形の 面積=半径×半径×314× 中 心 角 中 心 角 360 ° 弧の長さ=円周× 中 心 角 中 心 角 360 ° かずのかず 以上、「算数嫌いな おうぎ形の面積 90度のおうぎ形をイメージすれば、おうぎ形の面積も「元の円の面積」×おうぎ形の割合と分かりますね。 ( (図)) おうぎ形の面積=半径×半径×314× 中心角 360 上の2 半円の面積は、もとの円の面積の半分になりますね。 同様に、円を6等分してできた扇形の面積は、もとの円の面積の6分の1です。 このようにして、面積を求めたい 扇形はもとの円と




円 扇形 の面積 周や弧の長さの公式 数学fun



円すいの表面積 おうぎ形の中心角 簡単に求まります Net家庭学習支援塾
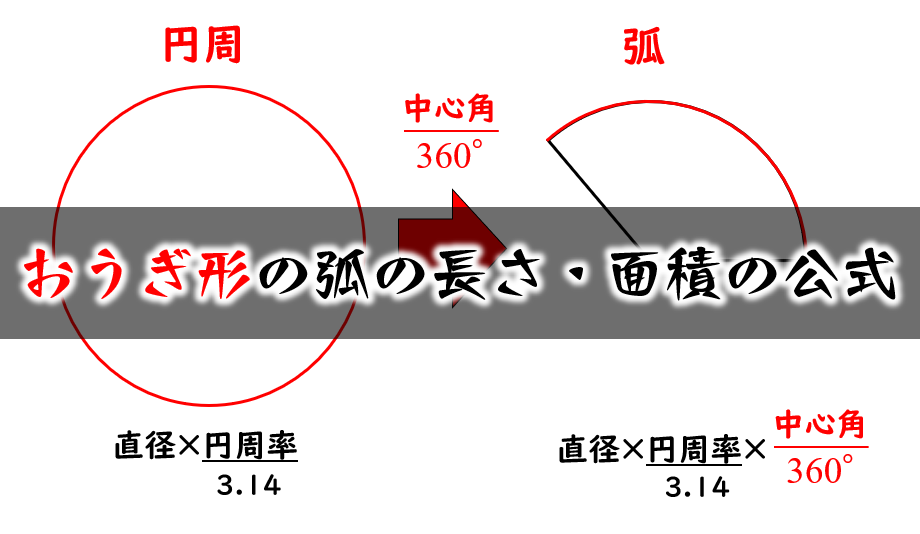
球の表面積と体積 このテキストでは、球の表面積と体積を求める公式を紹介します。2ページ目には練習問題を入れてあるので、チャレンジしてみてください。 表面積 まずは表面積です。 球の半径 完全な円の場合円周は 2πr 2 π r なので、弧の長さはこれに a 360 a 360 をかけた値になります。 『直径×314× 中心角 360 × 314 × 中 心 角 360 』⇒『2πr× a 360 2 π r × a 360 』 円の公式 円周・面積 円周率 = 3.14 円周の長さ = 直径 × 円周率 円周率 = 円周 ÷ 直径 おうぎ形の弧の長さ= 直径 × 314 × 中心角 ÷ 360 円の面積 = 半径 × 半径 × 円周率 弧の面積 =



Q Tbn And9gcs3ymdyzvot1 Cpwulrk43chbsfaz9pwdquufj4duocp3n3iv 01h T Usqp Cau



おうぎ形の面積と弧 計算が簡単にできる電卓サイト
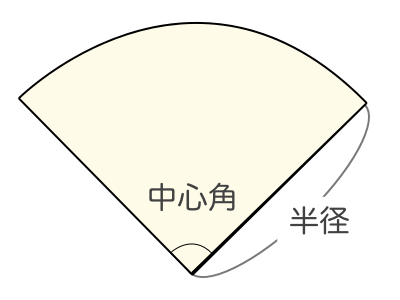
こちらも π を使うことで円と同様にスッキリ表すことができます。 半径 r 、中心角 α ° のおうぎ形の弧の長さ ℓ と面積 S 弧の長さ ℓ : ℓ = 2 π r × α 360 面 積 S : S = π r 2 × α 360おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時にどれくらいの割合なのか ということ。 たとえ練り合う 1つの円では、おうぎ形の弧の長さや面積の比は、中心角の大きさの比と 等しくなることを理解する。 ① (おうぎ形の弧の長さ) : (円の周の長さ) = (中心角の大きさ) : 360 ② (おうぎ形



半円と扇形が重なってる部分の面積の求め方どうやったら良いですか 黒く塗 Yahoo 知恵袋



標準 おうぎ形と正方形の面積 なかけんの数学ノート
扇(おうぎ)の面積 扇の面積を「S」としたとき、Sは次の公式で求めることができます。 これも同じように、円の面積を求める公式を思い出してください。 円の面積=r² π で求めることができま半径 ㎝、弧の長さ cmのおうぎ形の中心角を求めなさい。 おうぎ形の弧の長さが与えられているので こちらの公式を利用します。 まずは、半径6㎝の円の円周の長さを求めます。 そして、公式にそ a×d=b×c という形になるね。 これをおうぎ形に使ってみよう。 おうぎ形で比例式を使うときは、調べたいおうぎ形と半径が同じ円を考えましょう。 つまり、 この2つで考えるとい




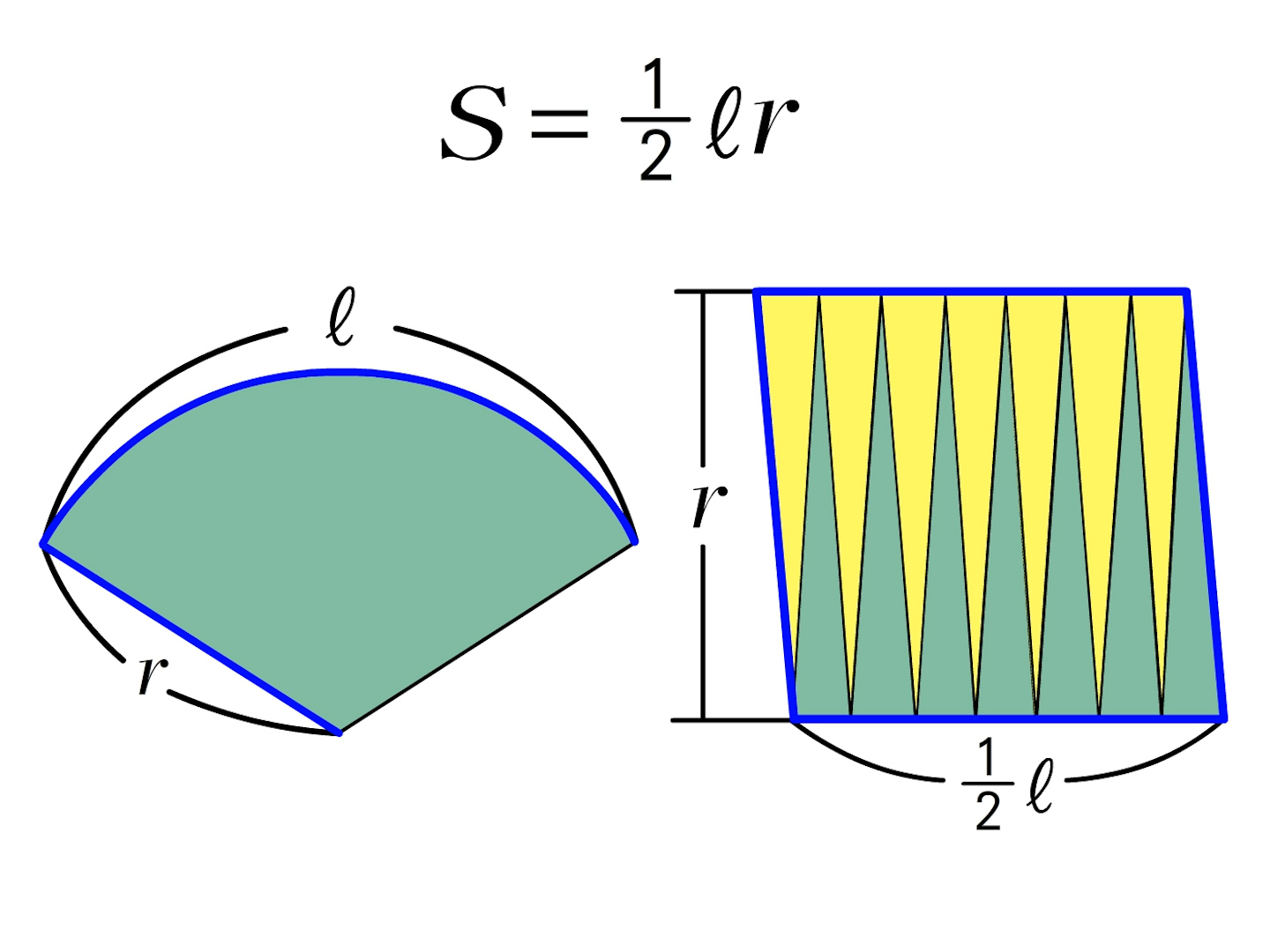
なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか
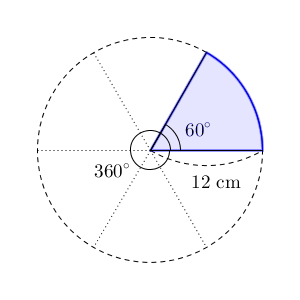
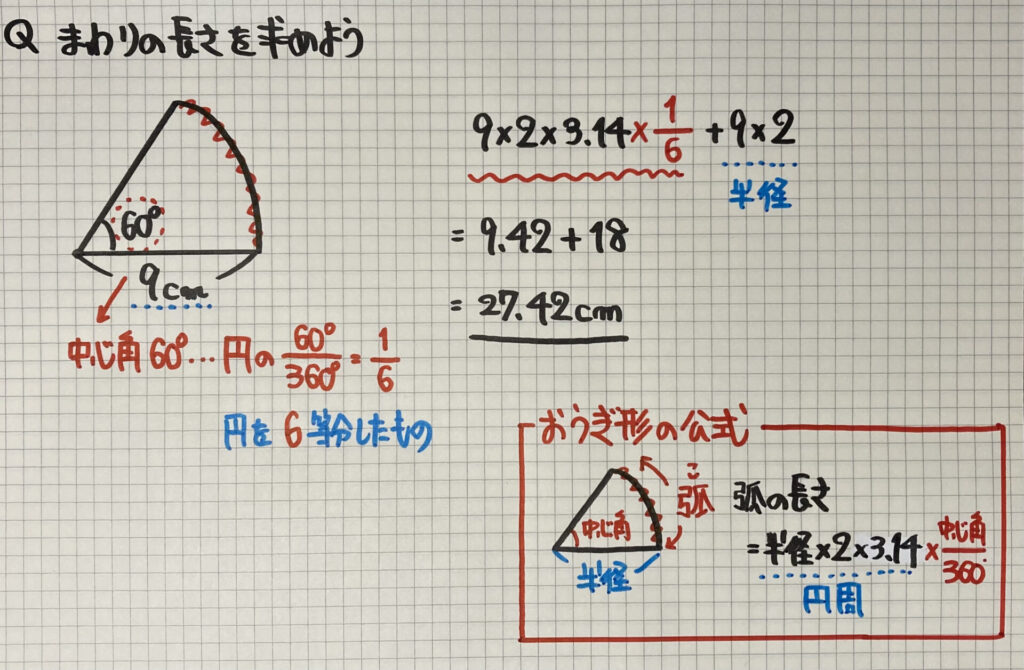
3 × 2 × 314 = 14 c m おうぎ型の弧の長さ (問題文より 314 c m )を比べると 314 ÷ 14 = 1 6 よって、おうぎ型は元の円の 1 6 の大きさとなります。 計算のコツ 円周率 314 等電卓の使い方 おうぎ形の半径と中心角を入力して「計算」ボタンを押すと、おうぎ形の面積と弧の長さが計算されます。 円周率は変更できます。 円周率で「πを使う」にチェックを入れると円周率扇形の面積は、r 2 θ/2で計算できます。 rは半径、θは角度(ラジアン)です。 なお、円の面積はπr^2ですね。 扇形の面積の公式に、θ=2πを代入すると円の公式と同じになります。 今回は扇




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




おうぎ形 面積 中心角 弧の長さの求め方 公式と裏ワザも紹介 トムラボ



面積の考え方 算数の教え上手 学びの場 Com



Q Tbn And9gctb22e4pxyd3p9h4fwinozohigm6unmhezvngmxg7ev6qlie8acoyo5 Usqp Cau



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun



小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ



中1数学です 図のおうぎ形の弧の長さは 同じ半径の円の周の何倍です Yahoo 知恵袋




円 扇形 の面積 周や弧の長さの公式 数学fun
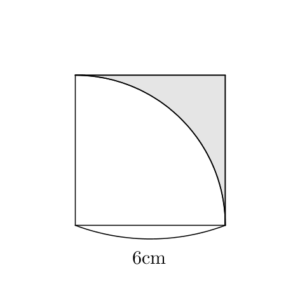



標準 おうぎ形と正方形の面積 なかけんの数学ノート



Q Tbn And9gctm68kdraeqpo Giyvxsau9prclg93urr7 Jafgpxhgzzohnnqrfkmb Usqp Cau




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ
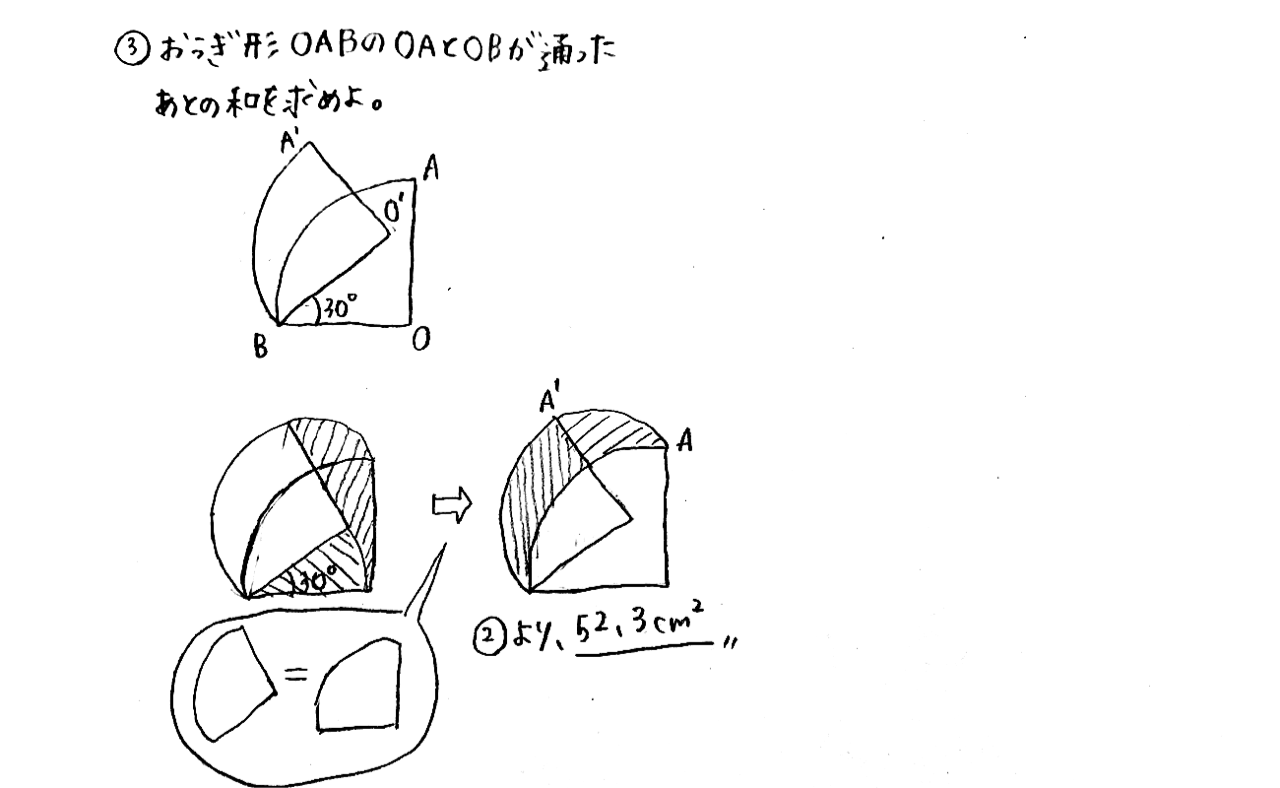



回転 扇形 算数ママの中学受験




円 扇形 の面積 周や弧の長さの公式 数学fun



2




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか
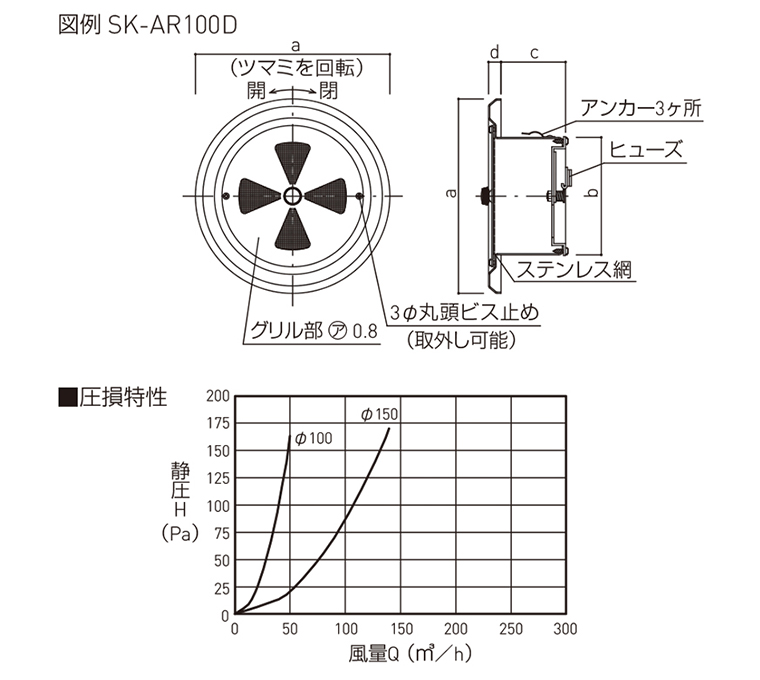



最大54 オフ 神栄ホームクリエイト 角型レジスター 防火ダンパー付 Smr 1d 300 350 Fucoa Cl



2



小5アタックの算数が難しくなる時期が来ました ひのき登戸教室ブログ 街の進学塾奮戦記



小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ
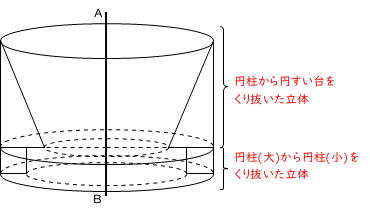



第547回 共学校の立体図形 1 前田昌宏の中学受験が楽しくなる算数塾




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題



1年 おうぎ形の面積 数学イメージ動画集 大日本図書
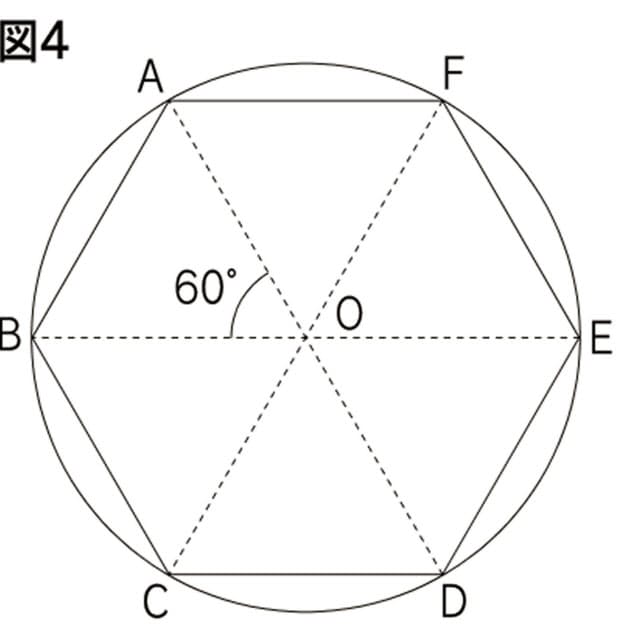



子供に説明できる 円の面積の公式 の証明 Nikkei Style
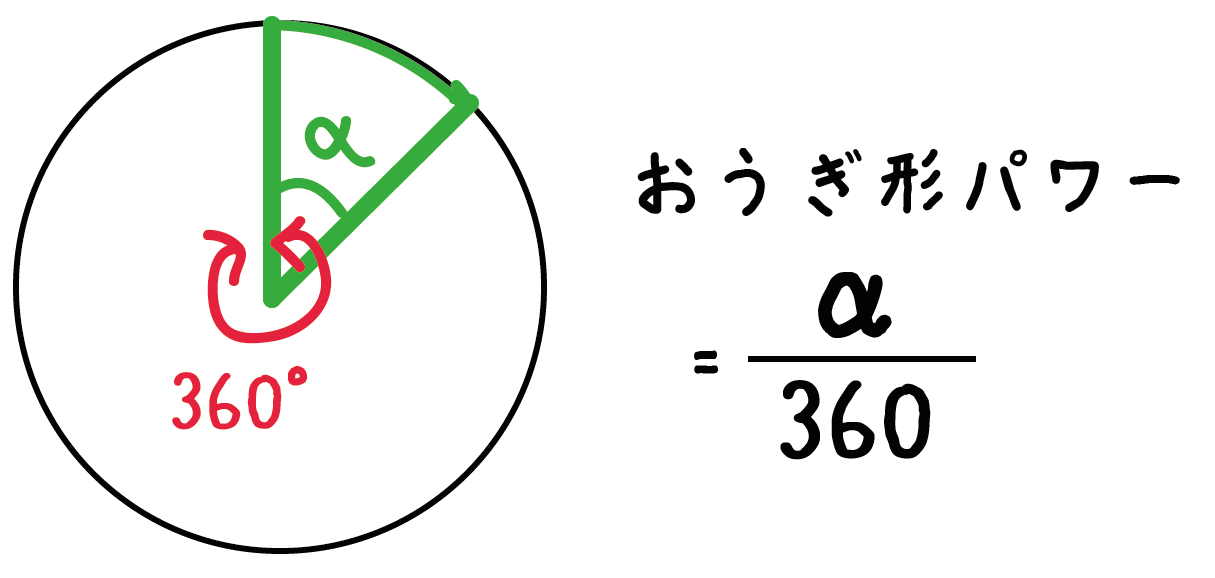



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ
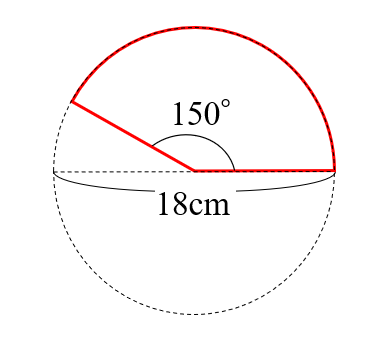



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
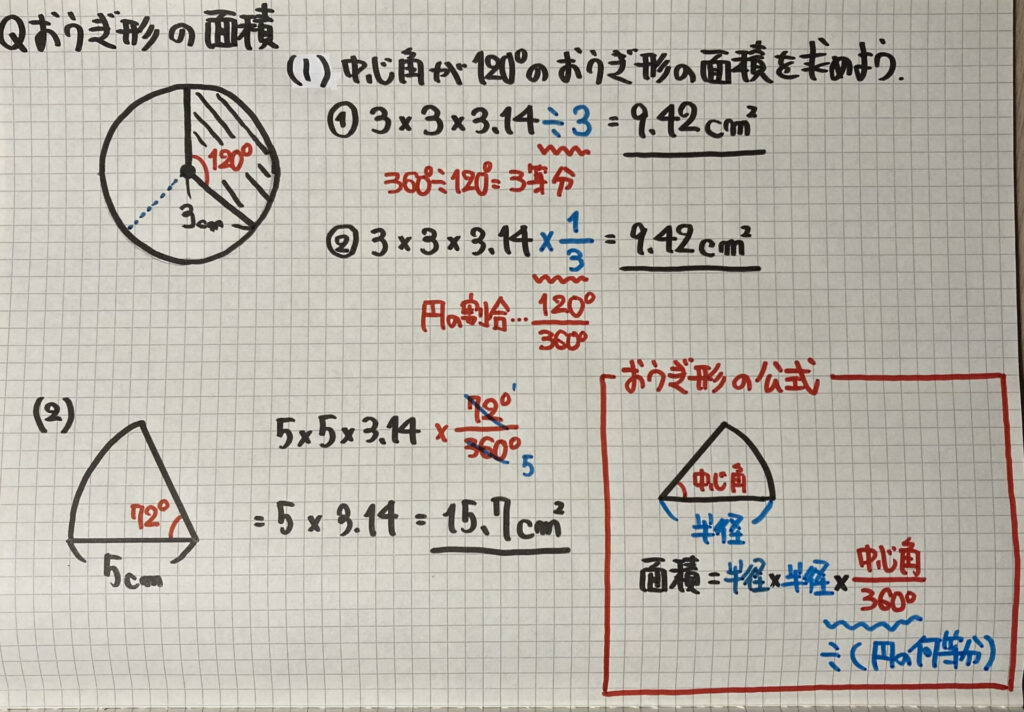



小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ




円 扇形 の面積 周や弧の長さの公式 数学fun



扇形の面積 小6です もう全くわかりません 問題はおうぎ形の中心 Yahoo 知恵袋




円 扇形 の面積 周や弧の長さの公式 数学fun



円 扇形に関連する面積の計算 理数系学習サイト Kori




扇形の面積の求め方 公式と計算例
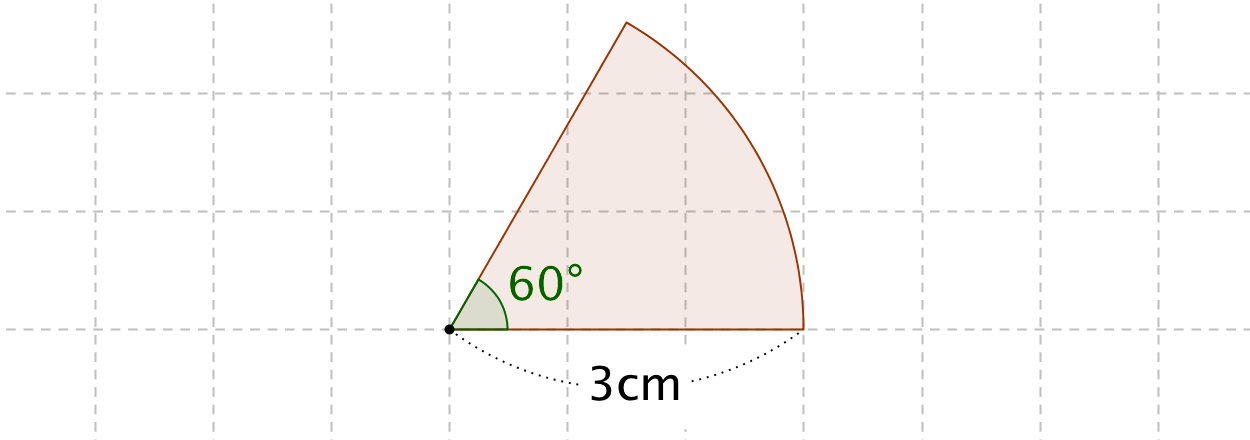



おうぎ形の面積の公式 算数の公式



問題93おうぎ形の面積




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか
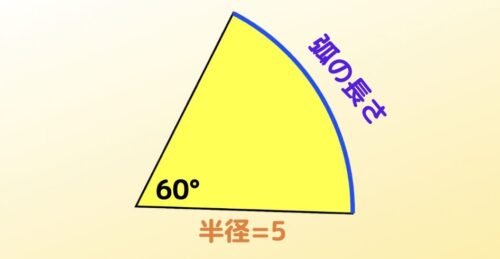



おうぎ形 面積 中心角 弧の長さの求め方 公式と裏ワザも紹介 トムラボ



問題93おうぎ形の面積




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか



2



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋




愛媛県 令和4年度数学 過去問 解答 家庭教師のやる気アシスト
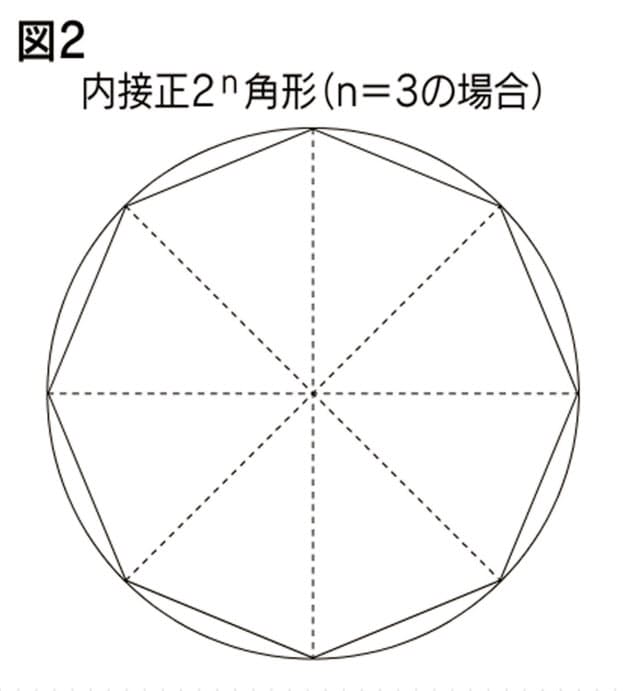



子供に説明できる 円の面積の公式 の証明 Nikkei Style




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




算数 本当に 分かる という事 おうぎ形の面積その1 エース学院




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ



Q Tbn And9gcsva1v8xokxd7vxf7z312hzc0yap4cangl4 Nsxy2 P6cynhkxwrzun Usqp Cau




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ
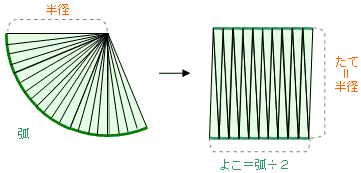



面積の考え方 算数の教え上手 学びの場 Com
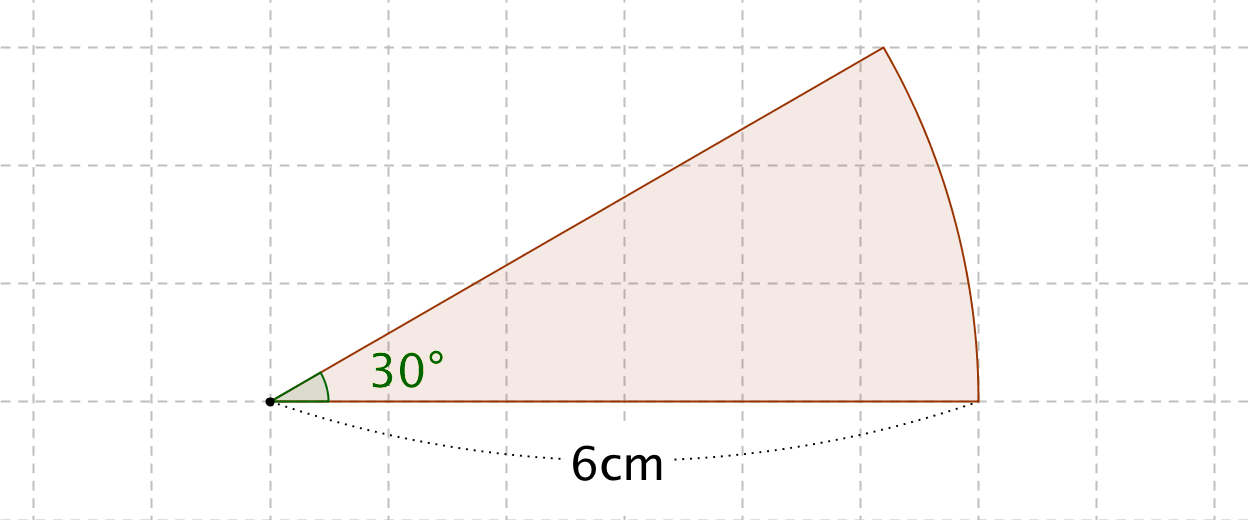



おうぎ形の面積の公式 算数の公式
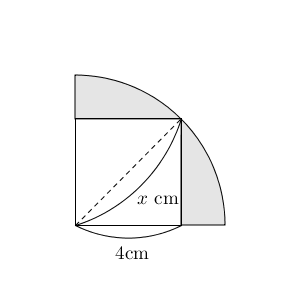



応用 おうぎ形と正方形の面積 なかけんの数学ノート




おうぎ形 面積 中心角 弧の長さの求め方 公式と裏ワザも紹介 トムラボ



問題93おうぎ形の面積




小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ



問題93おうぎ形の面積




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ



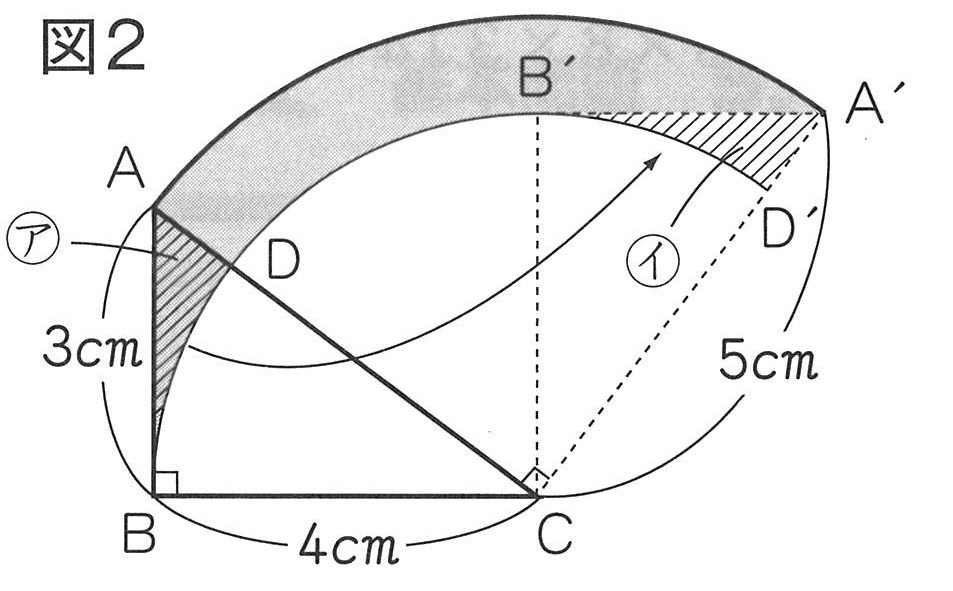
写真の問題の解答には面積差 ア イ 扇形の面積 長方形の面積となっています Yahoo 知恵袋




第547回 共学校の立体図形 1 前田昌宏の中学受験が楽しくなる算数塾
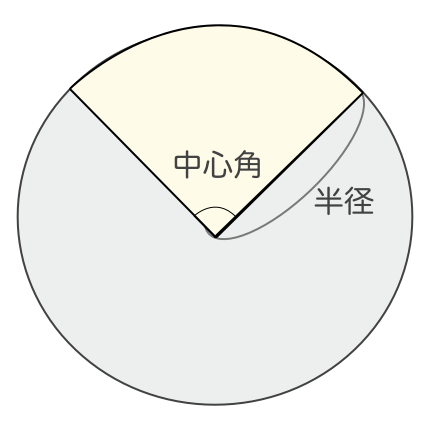



おうぎ形の面積と弧 計算が簡単にできる電卓サイト




難しい問題の解き方 の解説 円とおうぎ形の周りの長さ 面積を求める応用問題3選 中学受験ナビ




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




美和柄素材 扇散らし おうぎちらし Japanese Mon Iuen
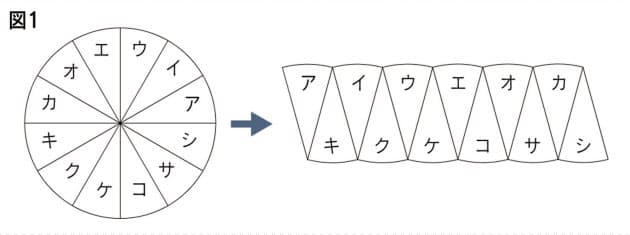



子供に説明できる 円の面積の公式 の証明 Nikkei Style
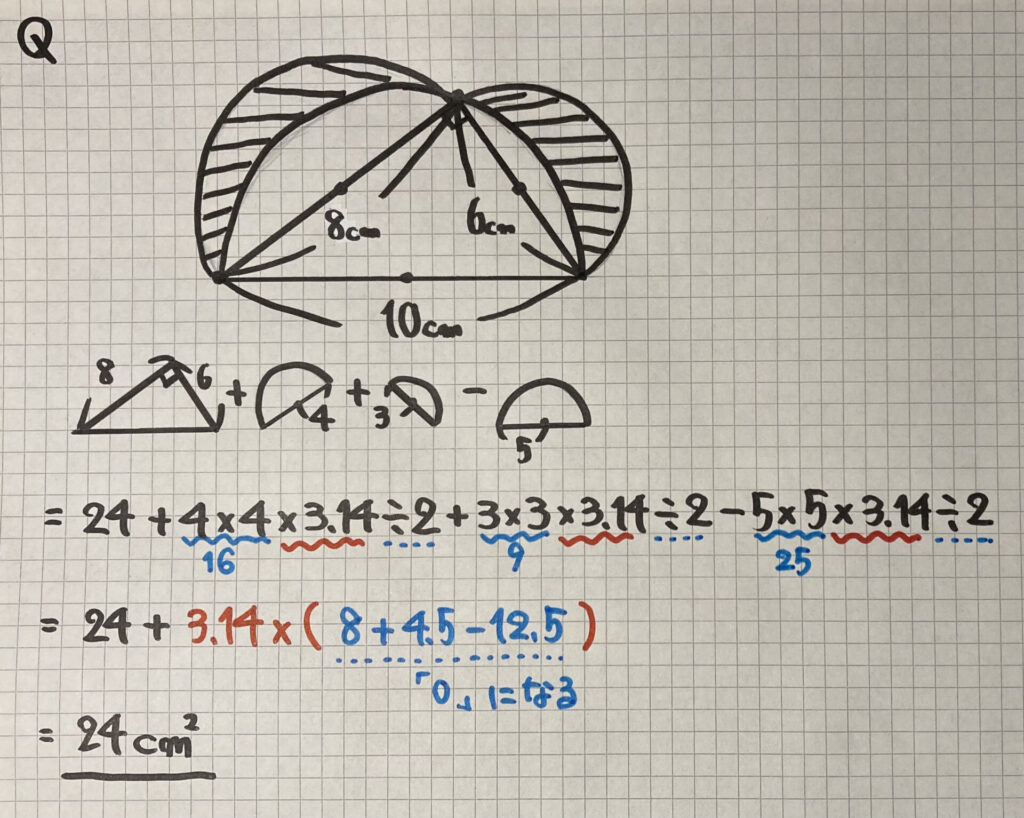



小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ
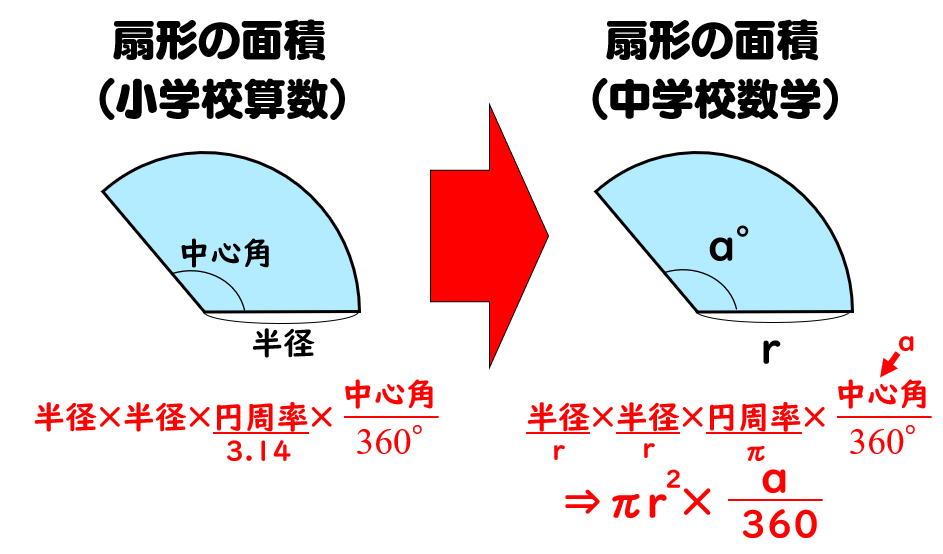



円 扇形 の面積 周や弧の長さの公式 数学fun




美和柄素材 扇散らし おうぎちらし Japanese Mon Iuen
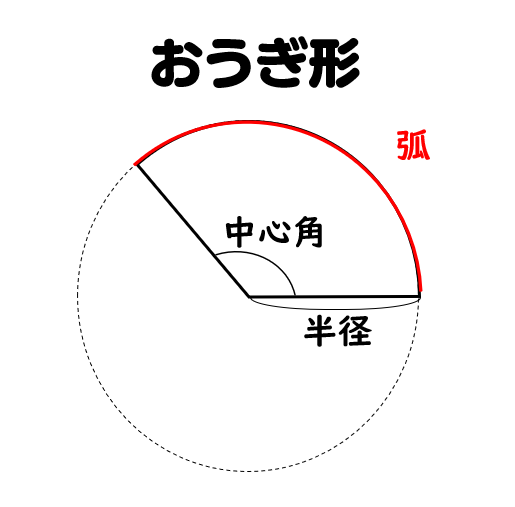



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun



円とおうぎ形 中学受験 田中貴 Com




三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
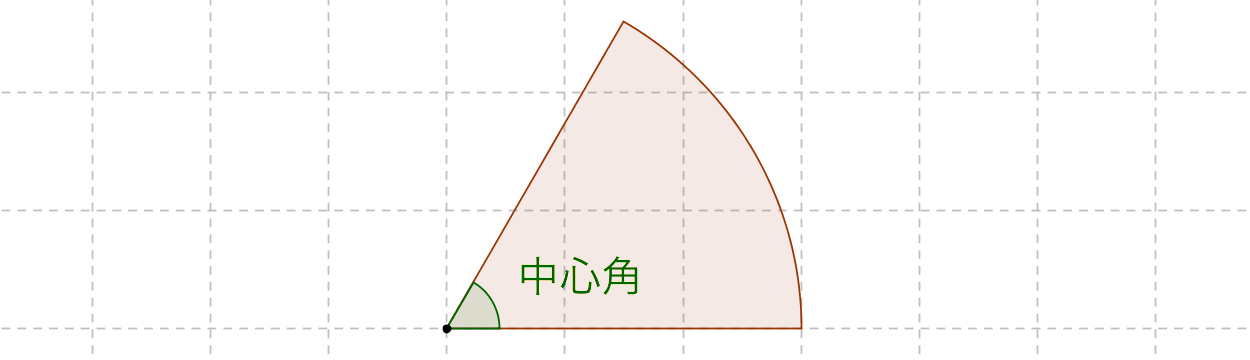



おうぎ形の面積の公式 算数の公式
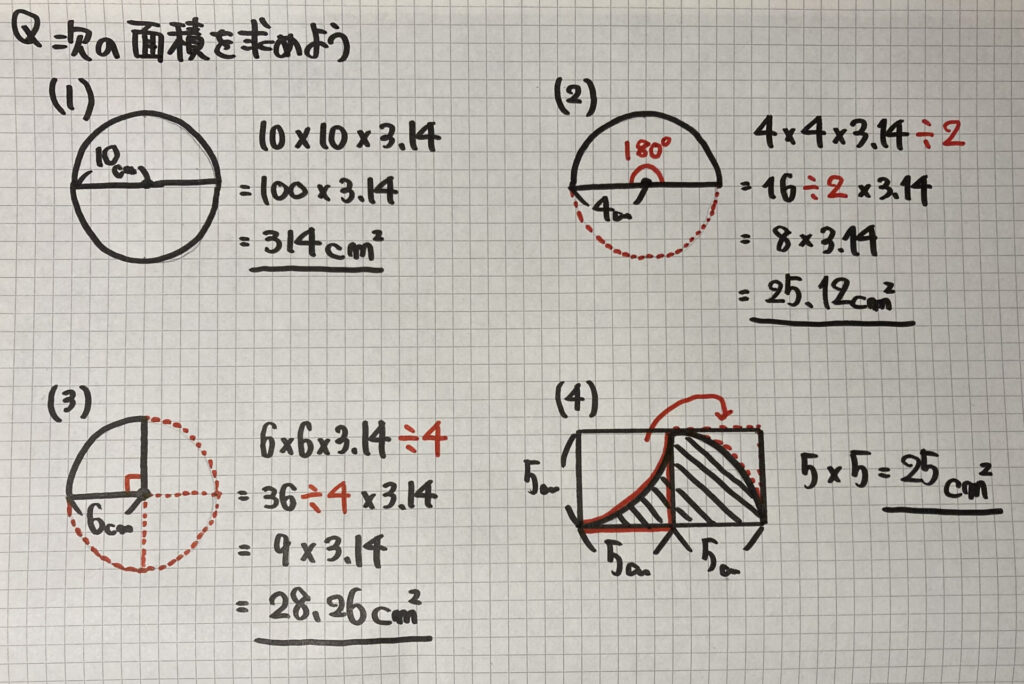



小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ
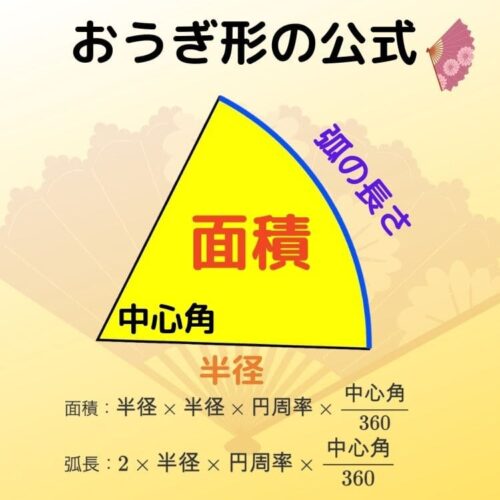



おうぎ形 面積 中心角 弧の長さの求め方 公式と裏ワザも紹介 トムラボ




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ




小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun



扇形の面積 三角形の面積について



2




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
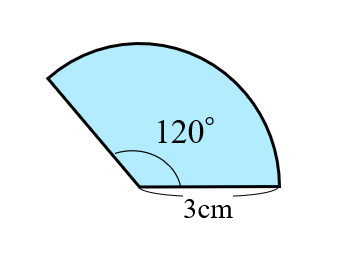



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




ホームズ Shell Du Maison Iv 2ldk 1階 56 07 賃貸マンション住宅情報



円すいの表面積 おうぎ形の中心角 簡単に求まります Net家庭学習支援塾




おうぎ形 面積 中心角 弧の長さの求め方 公式と裏ワザも紹介 トムラボ
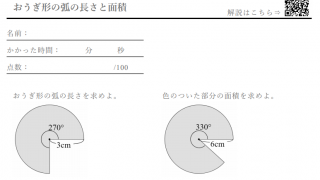



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




扇形の面積の求め方 公式と計算例
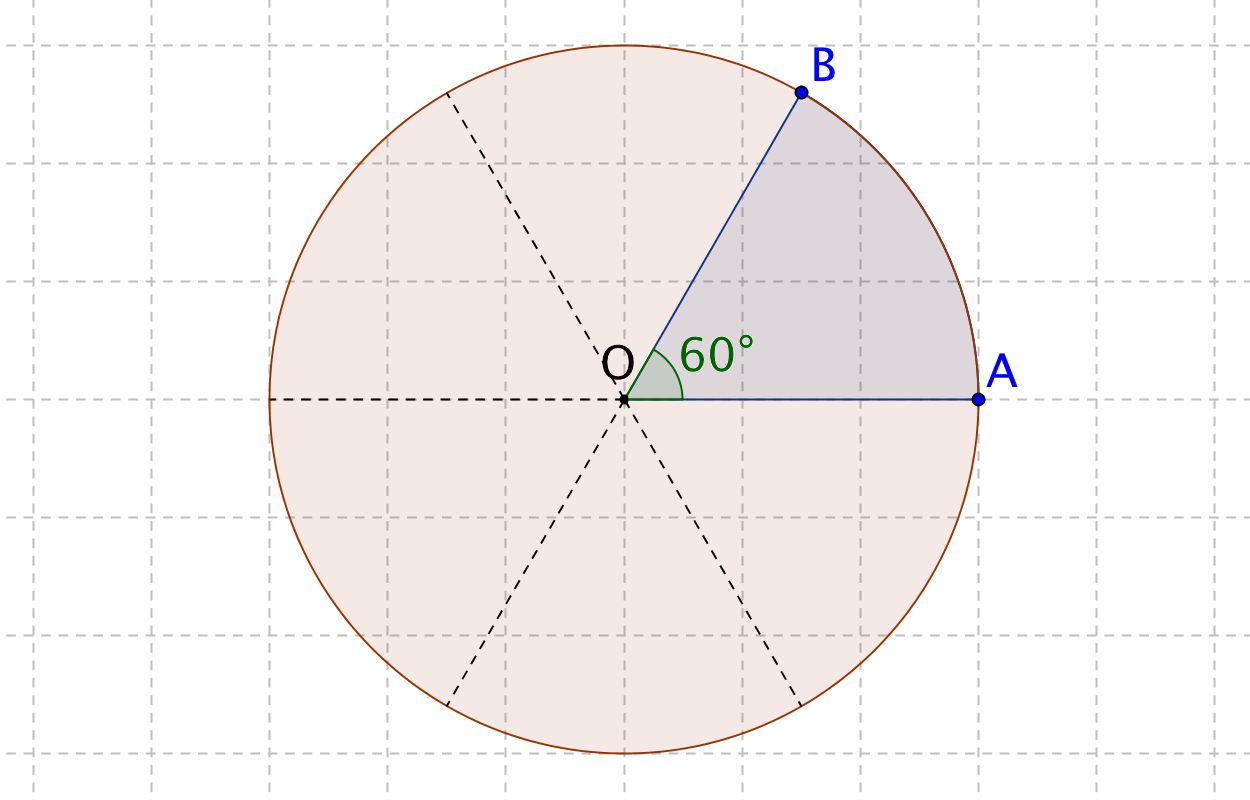



おうぎ形の面積の公式 算数の公式




円 扇形 の面積 周や弧の長さの公式 数学fun



おうぎ形の面積の求め方を教えてください 公式忘れたけど 半径7cmの円 Yahoo 知恵袋



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿