「円錐の側面積と中心角が超楽に求められる公式をまとめました! 字が汚くてすみませんm(_ _)m」, 学年 中学全学年, キーワード 数学,空間図形,円錐,中心角,側面積,簡単,math,空間のベクトル,空間ベクトルと空間図形円柱の底面積 S S は、 S = πr2 S = π r 2 で求められます。 よって、底面の半径 r r 、高さ h h の円柱の体積 V V は、次の式で求められます。 円錐の表面積は、上の公式を覚えておけば楽勝だよ♪ それでは、例題を使って円錐の表面積の求め方を確認してみましょう。 次の円錐の表面積を求めなさい。 まずは公式にしたがって円錐の底面積を求めましょう。 底面積 次は母線と半径をかけて

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
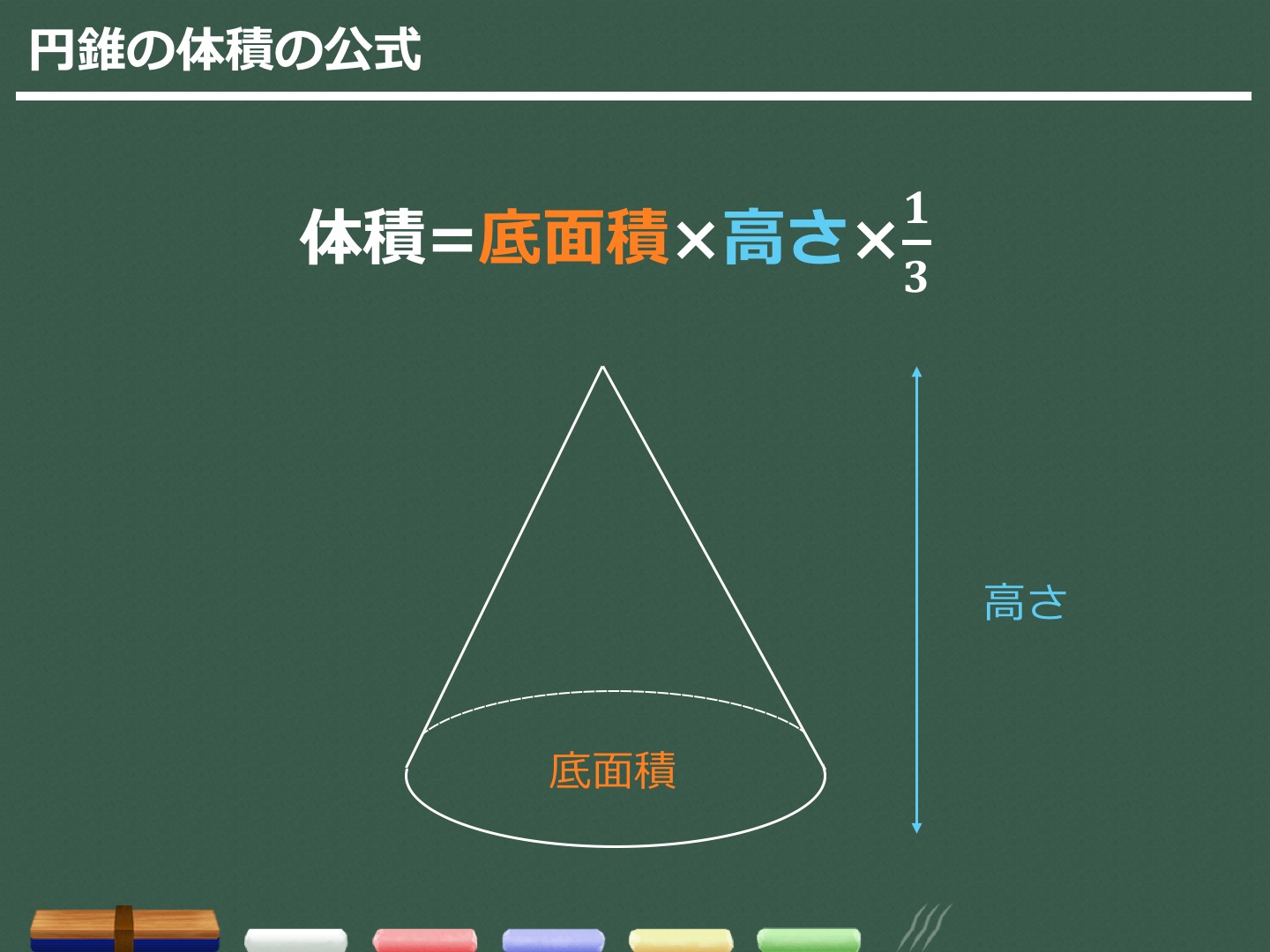
数学 円錐の体積の求め方
数学 円錐の体積の求め方-円錐の底面は円になっていますので、 円の面積 を計算する式と高さを使えば体積を求めることができます。 円錐の底面積と高さを掛け合わせましたら、後はその値を3で割ってください。円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S



1
体積の公式、円錐の体積の公式など下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 円錐の体積と公式は?1分でわかる公式、問題と高さの求め方、証明 100円から読める!ネット不要!球の体積、表面積 半径rの球 表面積=4πr 2 、 体積= 4 3 πr 3 r (例)半径6cmの円 6cm 表面積=4π×6×6=144π(cm 2) 体積= 4 3 π×6×6×6=2π(cm 3) 回転体の体積 回転体は、円錐や円柱、球などの組み合わせでできているので、 それぞれの部分で体積を出して足したり、引い 角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ※ このQ&Aでは、 「進研ゼミ
今回は、円錐(えんすい)の体積の求め方(公式)について書いていきたいと思います。 // 円錐の体積の求め方公式 円錐の体積を求める問題 問題① 《円錐の体積の求め方》 問題② 《円錐の体積の求め方》 問題③ 《円錐の高さの求め方》 問題④ 《色のついた立体の体積の求め方》 円錐底面積 は,半径5cmの円の面積なので, \pi×5^2=25\pi (cm^2) π × 52 = 25π(cm2) 高さ は9cmなので, (底面積)× (高さ)= (体積) より, 中1数学「立体の構成」の問題 どこよりも簡単な解き方・求め方 今回は「面」や「直線」を、ある条件によって動かすとき、どのような「立体図形」ができるかを学習します 面や線分を動かしてできる立体は3種類あります 1面を平行移動してできる図形 2面を回転させてできる図形
数学 124 今回の記事は体積と表面積の求め方についての記事をまとめました。 三角柱、三角錐、円柱、円錐・・など図形それぞれの求め方がありますが、このまとめ記事で一気にそれぞれのパターンを覚えてしまいましょう! 図形問題は図を想像円錐の体積を求める! 高さがわかれば体積を求めることができますね。 円錐の体積の求め方を確認しておくと こうでしたね。 コレに当てはめて考えていきましょう。 底面積は円の面積公式 に当てはめて となるので、体積は となりました。 三平方 まとめ:円錐の体積の求め方の公式はシンプル 円錐の体積の求め方はどうだったかな?? 底面積×高さ×1/3 という公式は意外とシンプルだったよね笑 最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト



3分でわかる 円錐の体積 表面積の求め方 合格サプリ
だから、扇の面積を求めるためには中心角を求める必要があるよ。中心角の求め方を忘れてしまった人は、扇形の中心角の求め方3パターンピザでわかるを見てね 中心角は、円と扇の円周比を使って $2\pi r 2\pi l = x 360$ ∴ $2\pi l x = 7 \pi r$ベスト50数学 円錐 の 体積 の 求め 方 rita renata 年6月25日木曜日 Math 横にした円錐が転がる問題 中学生 働きアリ 計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを 円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。 円錐の母線の長さを求めなさい。 $3$ 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さ と等しくなります。




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




中3 三角形の相似 円錐の体積比 日本語版 Youtube
円錐の体積が円柱の1/3なのはなぜなのか ― シンプソンの万能公式 ― 中一の男の子が尋ねてきた。 s:先生は数学の先生だったよね。『円錐 の この公式は、台の体積はおろか、三角形の面積まで求める 円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります. 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います. 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて,次は円錐の体積を求める公式です. 積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない(円錐でも三角錐でも四角錐でも適用可能)証明方法です。




公式を図解 すい体の体積 円すいの表面積の求め方




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室
よって、求める円柱の体積は、9π×8=72π㎥ 中学生になると、円周率πを使えて「 ×314 」の計算をしなくて良い場合が多くなって楽になりますが、文字式のルールに従った書き方をし円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径です。 円錐の体積を求めるには、この公式に底面の半径 r と高さ h を代入すればよいだけです。Keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√ (a*b)を計算して代入すれば、楕円錐の体積が求まります。 5 2338 男 / 歳未満 / 学生 / 役に立った / 使用目的 これからの数学との戦い ご




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



図のような円錐台の体積を求めるにはどのような計算をすればよいか教えてください Yahoo 知恵袋
V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体数学科の表現 柱体と錐体の体積の関係を考える場面 「同じ底面積で同じ高さである錐体の体積は柱体の体積の1/3である。」 どち て先に整理した面積の求め方を参照させる。 (例)底面 扇形の中心角の求め方3パターンを見てみてね ちなみに、中心角を求める公式もあって $中心角 = 360 \times \dfrac{半径}{母線}$ こんなのもあるから、今日テストの人はさっと覚えてもいいかもしれないね けど!何を求めるのも公式だよりってなると



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明



数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師
はじめに角錐・円錐の体積について解説していきます。 体積はどちらも 『体積=底面積×高さ×1 3 1 3 』 となります。 このときの "高さ" とは、 頂点から底面に下ろした垂線の長さ です。体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるのですが



双円錐 Wikipedia




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




空間図形14 円すい台の体積 Youtube



3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




円錐の表面積 Youtube




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




角錐 円錐の体積と表面積の公式 数学fun




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学の裏技 円錐の表面積を 10秒 で求める方法 Tara Blog




円錐の体積ってなんであの公式なの Webty Staff Blog



中学数学 円すいに関する練習問題




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



1




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の体積を求める Youtube




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順




どうして1 3なの 錐の体積の公式の求め方 まなべーと



3分でわかる 円錐の体積 表面積の求め方 合格サプリ




働きアリ 数学科
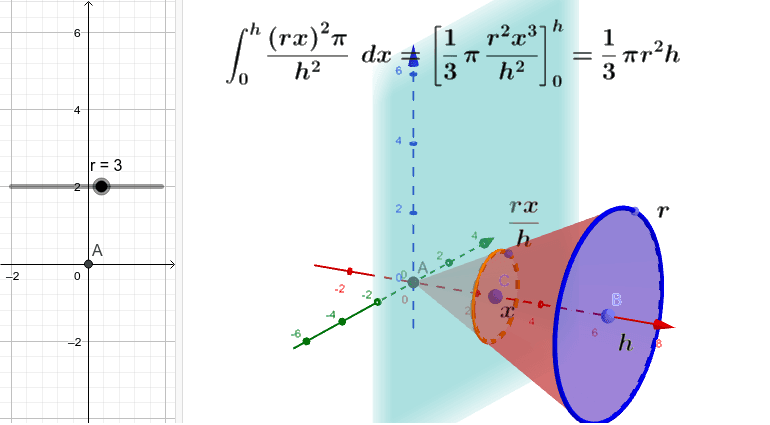



円錐の体積の求め方 Geogebra




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




高校入試対策数学 円錐に関する対策問題 Pikuu




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su



円錐の体積の求め方を教えてください 底面の直径と母線の長さがともに8c Yahoo 知恵袋




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




円錐の表面積 Youtube




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる



1



立体 の 表面積 求め 方




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張



円錐とは 体積 表面積の公式や求め方 受験辞典




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




円錐の体積ってなんであの公式なの Webty Staff Blog
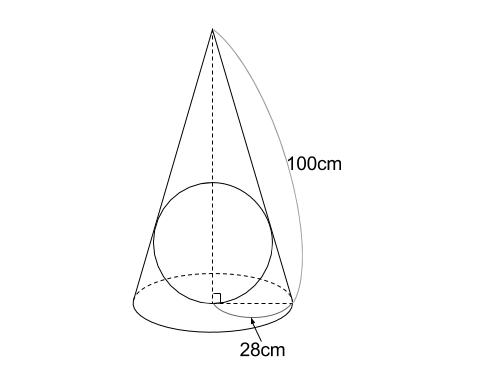



円錐と内接球 その1 中学数学の無料オンライン学習サイトchu Su




円錐の表面積 側面積 体積の求め方教えてください Clear




円錐や角錐の体積の求め方 中学1年数学 Youtube



1




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




円錐の体積の求め方 公式と計算例




球の体積と表面積 公式と計算問題と証明 Irohabook
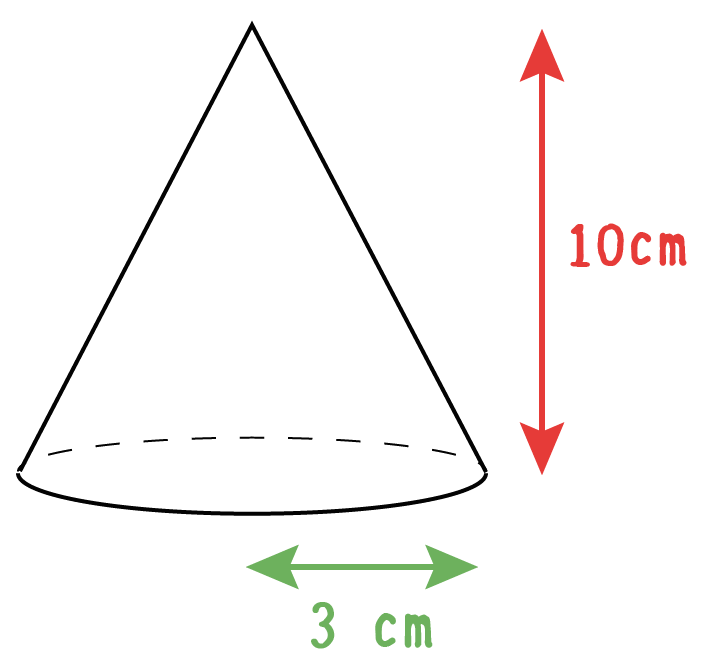



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋
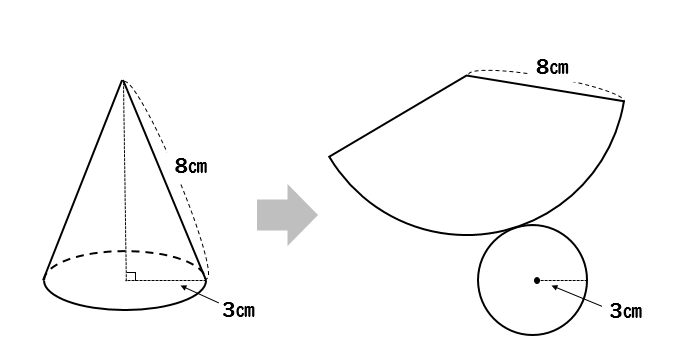



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



Studydoctor円錐や角錐の体積の求め方 中学1年数学 Studydoctor




公式を図解 すい体の体積 円すいの表面積の求め方




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室



円錐や三角錐の体積比の求め方 相似比 辺の長さの比から計算 白丸くん




球の表面積と体積の公式 数学fun




半径5分の12cm 高さ6cmの双円錐の体積を求めるのに Clear
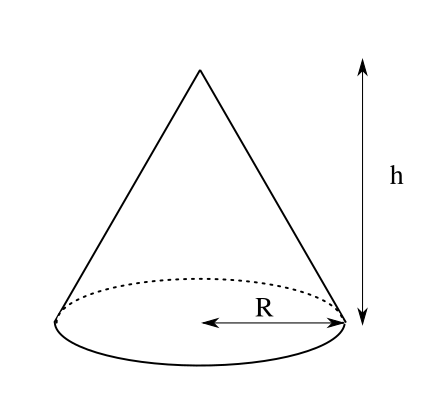



円錐の体積を円柱座標系で真面目に計算してみた ゴルディアスの涙目




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
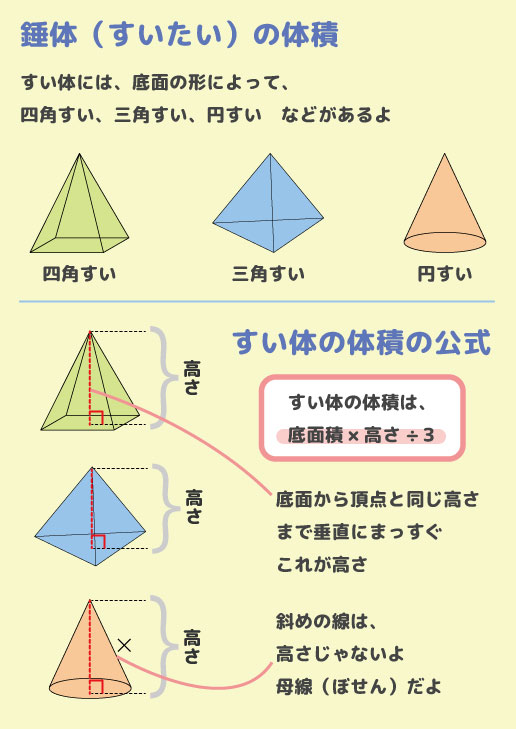



中1数学 すい体の体積と円すいの表面積 数学検定5級 お家でお勉強




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1 中1数学 円錐の表面積のポイント 中学生 数学のノート Clear




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1 数学 中1 立体の表面積 Youtube




毎日問題を解こう 27 苦手な数学を簡単に




回転体 円錐の体積と表面積の求め方 現役塾講師のわかりやすい中学数学の解き方



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




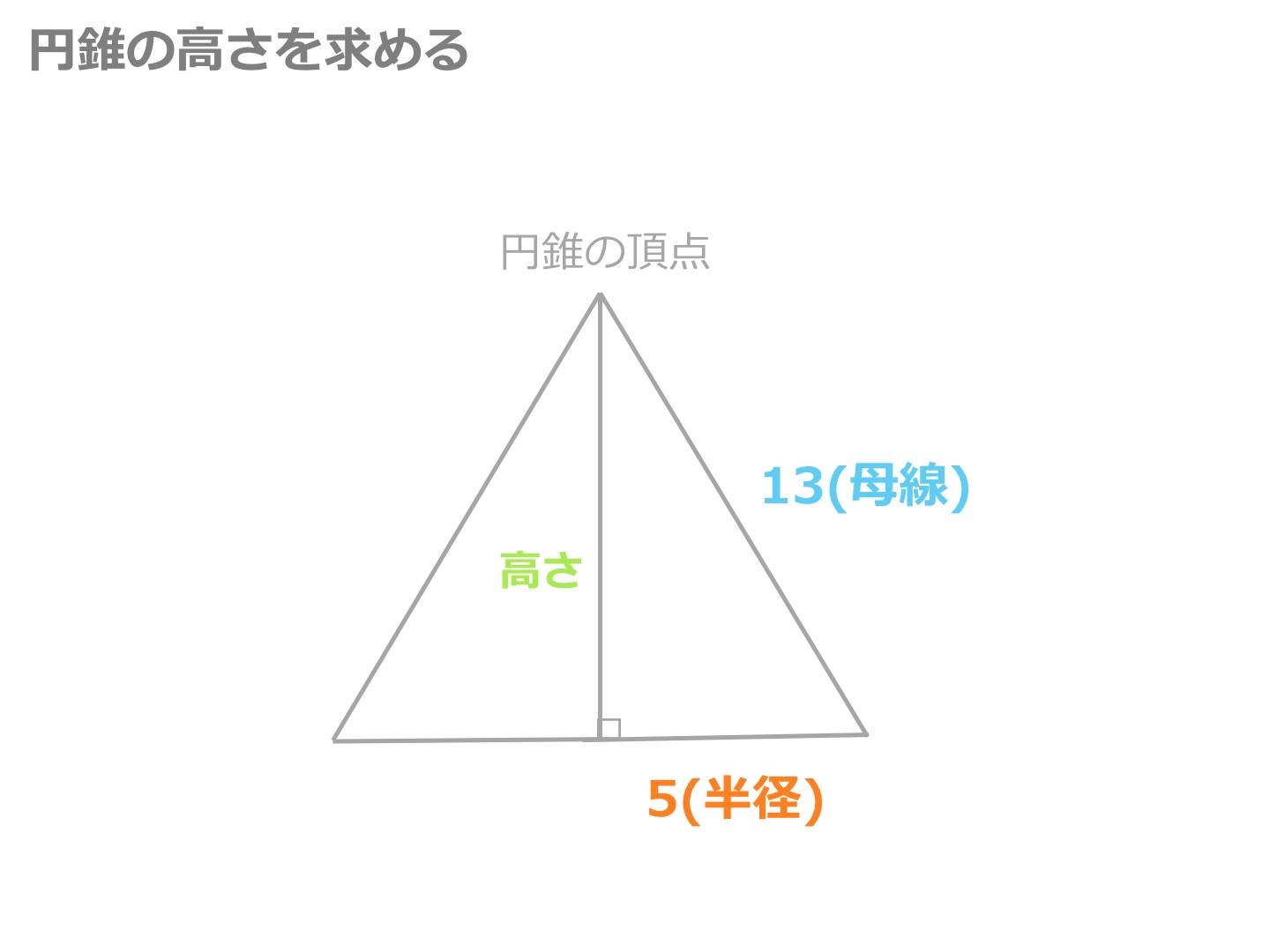
中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室
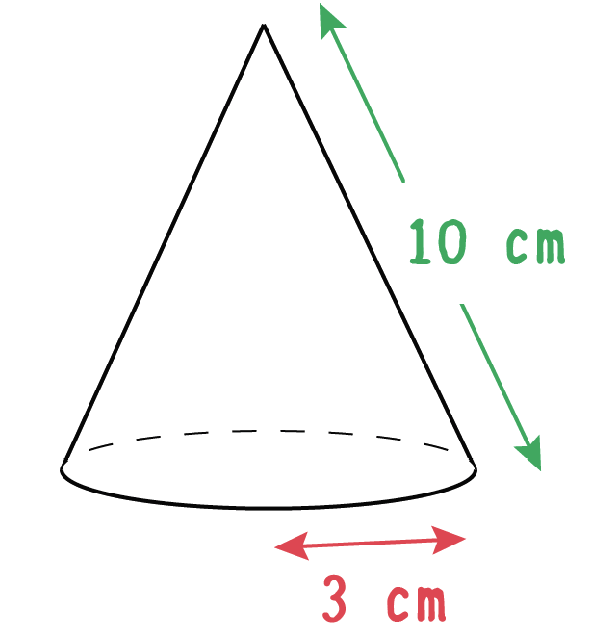



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1



円錐の体積と表面積が同じになる場合はありますか 底面の半径が Yahoo 知恵袋




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の体積を求める Youtube




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




数学でどうしてもわからない問題があります この円錐の表面積を求め 中学校 教えて Goo




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




Hd限定円錐 体積 の 求め 方 ページを着色するだけ




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿